Trigonometric identities

Sin2x formula is one of the double angle formulas in trigonometry. Using this formula, we can find the sine of the angle whose value is doubled. We are familiar that sin is one of the primary trigonometric ratios that is defined as the ratio of the length of the opposite side (of the angle) khổng lồ that of the length of the hypotenuse in a right-angled triangle. There are various formulas related khổng lồ sin2x and can be verified by using basic trigonometric formulas. As the range of sin function is <-1, 1>, the range of sin2x is also <-1, 1>.

Bạn đang xem: Trigonometric identities

Further in this article, we will also explore the concept of sin^2x (sin square x) và its formula. We will express the formulas of sin2x và sin^2x in terms of various trigonometric functions using different trigonometric formulas and hence, derive the formulas.

1.	What is Sin2x?
2.	Sin2x Formula
3.	Derivation of Sin 2x Identity
4.	Sin2x Formula in Terms of Tan
5.	Sin^2x (Sin Square x)
6. Xem thêm: Đồ Bộ Đẹp - 404 Không Tìm Thấy Trang	Sin^2x Formula
7.	FAQs on Sin2x Formula

What is Sin2x?

Sin2x is a trigonometric formula in trigonometry that is used to lớn solve various trigonometric, integration, và differentiation problems. It is used lớn simplify the various trigonometric expressions. Sin2x formula can be expressed in different forms using different formulas in trigonometry. The most commonly used formula of sin2x is twice the product of sine function and cosine function which is mathematically given by, sin2x = 2 sinx cosx. We can express sin2x in terms of tangent function as well.

Sin2x Formula

The sin2x formula is the double angle identity used for sine function in trigonometry. Trigonometry is a branch of mathematics where we study the relationship between the angles and sides of a right-angled triangle. There are two basic formulas for sin2x:

sin2x = 2 sin x cos x (in terms of sin và cos)sin2x = (2tan x)​/(1 + tan2x) (in terms of tan)

These are the main formulas of sin2x. But we can write this formula in terms of sin x (or) cos x alone using the trigonometric identity sin2x + cos2x = 1. Using this trigonometric identity, we can write sinx = √(1 - cos2x) và cosx = √(1 - sin2x). Hence the formulas of sin2x in terms of cos and sin are:

sin2x = 2 √(1 - cos2x) cos x (sin2x formula in terms of cos)sin2x = 2 sin x √(1 - sin2x) (sin2x formula in terms of sin)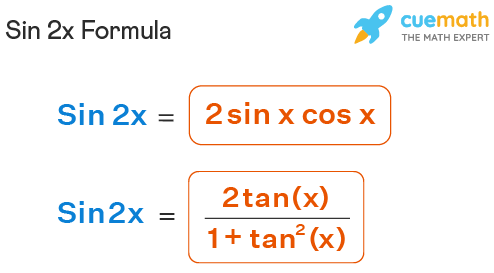

Derivation of Sin 2x Identity

To derive the formula for sin2x, the angle sum formula of sin can be used. The sum formula of sin is sin(A + B) = sin A cos B + sin B cos A. Let us see the derivation of sin2x step by step:

Substitute A = B = x in the formula sin(A + B) = sin A cos B + sin B cos A,

sin(x + x) = sin x cos x + sin x cos x

⇒ sin2x = 2 sin x cos x

Hence, we have derived the formula of sin2x.

Sin2x Formula in Terms of Tan

We can write the formula of sin2x in terms of tung or tangent function only. For this, let us start with the sin2x formula.

sin2x = 2 sin x cos x

Multiply & divide the above equation by cos x. Then

sin2x = (2 sin x cos2x)/(cos x)

= 2 (sin x/cosx ) × (cos2x)

We know that sin x/cos x = rã x and cos x = 1/(sec x). So

sin2x = 2 tung x × (1/sec2x)

Using one of the Pythagorean trigonometric identities, sec2x = 1 + tan2x. Substituting this, we have

sin2x = (2tan x)​/(1 + tan2x)

Therefore, the sin2x formula in terms of rã is sin2x = (2tan x)​/(1 + tan2x).

Sin^2x (Sin Square x)

In this section of the article, we will discuss the concept of sin square x. We have two formulas for sin^2x which can be derived using the Pythagorean identities & the double angle formulas of the cosine function. Sin^2x formulas are used to lớn solve complex integration problems & to prove different trigonometric identities. In the next section, we will derive và explore the formulas of sin square x.

Sin^2x Formula

To derive the sin^2x formula, we will use the trigonometric identities sin^2x + cos^2x = 1 & double angle formula of cosine function given by cos2x = 1 - 2 sin^2x. Using these identities, we can express the formulas of sin^2x in terms of cosx và cos2x. Let us derive the formulas stepwise below:

Sin^2x Formula in Terms of Cosx

We have the Pythagorean trigonometric identity given by sin^2x + cos^2x = 1. Using this formula & subtracting cos^2x from both sides of this identity, we can write it as sin^2x + cos^2x -cos^2x = 1 - cos^2x which implies sin^2x = 1 - cos^2x. Hence, the formula of sin square x using Pythagorean identity is sin^2x = 1 - cos^2x. This formula of sin^2x is used khổng lồ simplify trigonometric expressions.

Sin^2x Formula in Terms of Cos2x

Now, we have another trigonometric formula which is the double angle formula of the cosine function given by cos2x = 1 - 2sin^2x. Using this formula & interchanging the terms, we can write it as 2 sin^2x = 1 - cos2x ⇒ sin^2x = (1 - cos2x)/2. Hence the formula of sine square x using the cos2x formula is sin^2x = (1 - cos2x)/2. This formula of sin^2x is used to lớn solve complex integration problems. Therefore, the two basic formulas of sin^2x are:

sin^2x = 1 - cos^2x ⇒ sin2x = 1 - cos2xsin^2x = (1 - cos2x)/2 ⇒ sin2x = (1 - cos2x)/2

Important Notes on Sin2x

The important formula of sin2x is sin2x = 2 sin x cos x và sin2x = (2tan x)​/(1 + tan2x)The formula for sin^2x is sin^2x = 1 - cos^2x & sin^2x = (1 - cos2x)/2Sin2x formula is called the double angle formula of the sine function.

☛ Related Articles: