Tính chất vecto trong tam giác

Định nghĩa: mang đến hai vectơ (overrightarrowa), (overrightarrowb). Mang một điểm (A) tùy ý, vẽ (overrightarrowAB) = (overrightarrowa), (overrightarrowBC) = (overrightarrowb). Vectơ (overrightarrowAC) được hotline là tổng của hai vectơ (overrightarrowa) và (overrightarrowb).

Bạn đang xem: Tính chất vecto trong tam giác

(overrightarrowAC) = (overrightarrowa) + (overrightarrowb).

2. Nguyên tắc hình bình hành 

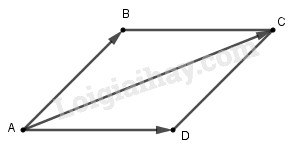
Nếu (ABCD) là hình bình hành thì 

(overrightarrowAB) + (overrightarrowAD) = (overrightarrowAC).

3. Tính chất của tổng các vectơ

- đặc thù giao hoán

(overrightarrowa) + (overrightarrowb) = (overrightarrowb) + (overrightarrowa)

- tính chất kết hợp

((overrightarrowa) + (overrightarrowb) ) + (overrightarrowc) = (overrightarrowa) + ((overrightarrowb) +(overrightarrowc))

- đặc điểm của (overrightarrow0):

(overrightarrowa)+(overrightarrow0) = (overrightarrow0) + (overrightarrowa) (=overrightarrowa)

4. Hiệu của nhị vectơ

a) Vec tơ đối: Vectơ gồm cùng độ dài cùng ngược phía với vec tơ (overrightarrowa) được call là vec tơ đối của vec tơ (overrightarrowa), kí hiệu (-overrightarrowa).

Xem thêm: Phim Vòng Vây Hoa Hồng Tập Cuối, Vòng Vây Hoa Hồng

Vec tơ đối của (overrightarrow0) là vectơ (overrightarrow0).

b) Hiệu của hai vec tơ: cho hai vectơ (overrightarrowa), (overrightarrowb). Vec tơ hiệu của nhị vectơ, kí hiệu (overrightarrowa)- (overrightarrowb) là vectơ (overrightarrowa) + (-(overrightarrowb))

(overrightarrowa)- (overrightarrowb) = (overrightarrowa) + (-(overrightarrowb)).

c) Chú ý: Với cha điểm bất kì, ta luôn có 

(overrightarrowAB) + (overrightarrowBC) = (overrightarrowAC) (1)

(overrightarrowAB) - (overrightarrowAC) = (overrightarrowCB) (2)

(1) là nguyên tắc 3 điểm (quy tắc tam giác) so với tổng của nhì vectơ.

(2) là quy tắc 3 điểm (quy tắc tam giác) đối với hiệu các vectơ.

5. Áp dụng 

a) Trung điểm của đoạn thẳng:

(I) là trung điểm của đoạn thẳng

⇔ (overrightarrowIA) +(overrightarrowIB) = (overrightarrow0)

b) giữa trung tâm của tam giác:

(G) là trung tâm của tam giác ∆ABC 

⇔ (overrightarrowGA) + (overrightarrowGB)+(overrightarrowGC) = (overrightarrow0)