Đạo hàm ln(x)^2
- Tính đạo hàm (y') sử dụng những công thức đạo hàm (left( u^n ight)' = nu'u^n - 1) với (left( ln u ight)' = dfracu'u)
- thay (x = e) vào đạo hàm vừa kiếm được và kết luận.
Bạn đang xem: Đạo hàm ln(x)^2
Ta có:
(y' = 2left< ln left( ln x ight) ight>'.ln left( ln x ight))
Mà $left< ln left( ln x ight) ight>^/ = dfracleft( ln x ight)^/ln x = dfracdfrac1xln x = dfrac1xln x.$
Suy ra $y^/ = 2.dfrac1xln x.ln left( ln x ight) = dfrac2ln left( ln x ight)xln x$ $ Rightarrow y^/left( e ight) = dfrac2ln left( ln e ight)e.ln e = dfrac2.ln 1e.ln e = 0$
LỘ TRÌNH ÔN THI ĐÁNH GIÁ NĂNG LỰC BÀI BẢN TỪ VỪNG ƠI!
Bạn đăng băn khoăn tìm hiểu tham gia thi không biết hỏi ai?
Bạn đề nghị lộ trình ôn thi bài xích bản từ những người dân am hiểu về kì thi cùng đề thi?
Bạn nên thầy cô đồng hành suốt quy trình ôn luyện?
Đấy là lý do Vừng ơi - yeahflashback.com đơn vị chức năng chuyên về ôn luyện thi reviews năng lực để giúp đỡ bạn:
Lộ trình chuyên nghiệp 5V: từ bỏ cơ bạn dạng -Luyện từng phần đề thi - Luyện đềPhủ bí mật lượng kỹ năng bởi khối hệ thống ngân sản phẩm 15.000 thắc mắc độc quyềnKết đúng theo học liên tưởng live, giáo viên chủ nhiệm hỗ trợ trong suốt thừa trìnhMiễn phí hỗ trợ tư vấn - TẠI ĐÂY
...
Bài tập gồm liên quan
Hàm số logarit Luyện Ngay
Nhóm 2K5 ôn thi đánh giá năng lực 2023 miễn phí
Theo dõi Vừng ơi trên


Đăng ký bốn vấn
Gửi thông tin
 |  |  |  |
 |  |  |  |
Câu hỏi liên quan
Hàm số (y = log _axleft( {0
Điểm nào sau đây không thuộc đồ thị hàm số (y = log _axleft( {0
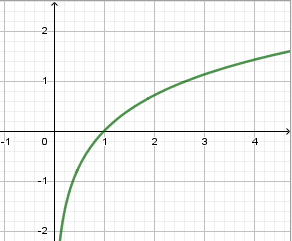
Tìm tập quý giá ( mT) của hàm số (fleft( x ight) = dfracln xx) với (x in left< 1;e^2 ight>.)
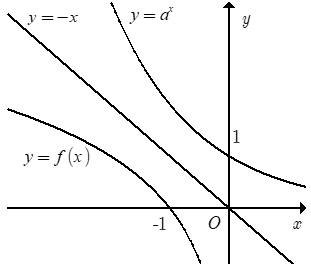
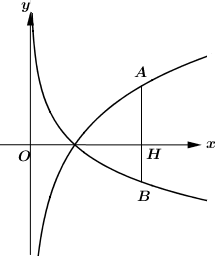
Biết nhì hàm số $y = a^x$ với $y = fleft( x ight)$ gồm đồ thị như hình mẫu vẽ đồng thời đồ dùng thị của nhị hàm số này đối xứng nhau qua đường thẳng $d:y = - x$. Tính $fleft( - a^3 ight).$
Tìm tất cả các cực hiếm của tham số (m) để hàm số (y = log _2020left( mx - m + 2 ight)) xác định trên (left< 1; + infty ight).)
Đồ thị của hàm số (y = fleft( x ight)) đối xứng với đồ gia dụng thị của hàm số (y = a^x,,left( a > 0,,,a e 1 ight)) qua điểm (Mleft( 1;1 ight)). Quý hiếm của hàm số (y = fleft( x ight)) trên (x = 2 + log _adfrac12020) bằng:
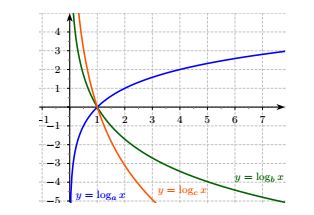
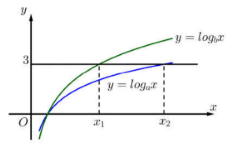
Cho (a) và (b) là những số thực dương không giống 1. Biết rằng bất kì đường trực tiếp nào tuy nhiên song cùng với trục tung mà cắt những đồ thị (y = log _ax,,,y = log _bx) và trục hoành thứu tự tại (A,,,B) cùng (H) rành mạch ta đều sở hữu (3HA = 4HB) (hình vẽ bên dưới). Khẳng định nào sau đây là đúng?
Cho nhị hàm số (y = ln left| dfracx - 2x ight|) với (y = dfrac3x - 2 - dfrac1x + 4m - 2020). Tổng toàn bộ các cực hiếm nguyên của tham số m nhằm hai thiết bị thị hàm số giảm nhau tại một điểm duy nhất bằng:
Cho $x, y$ là những số thực thỏa mãn (log _4left( x + y ight) + log _4left( x - y ight) ge 1). Tìm giá chỉ trị nhỏ tuổi nhất (P_min ) của biểu thức (P = 2x - y).
Trên khoảng ((0; + infty )), đạo hàm của hàm số (y = log _2x) là:
Tiếp đường của đồ gia dụng thị hàm số (y = 2^x + log left( 11 - x ight)) trên điểm (Mleft( 1;3 ight)) có thông số góc là











